399페이지 14번 부터 답변 드리겠습니다.

네, 이 문제는 조건에서 높이가 350[mm]인 각형 덕트를 구하는 조건이기 때문에 풀이를 할 때 주의해야 합니다.

A-B, B-C는 35cm의 단변(높이)으로 환산표에서 구하면 됩니다.

C-D 구간은 환산표에서 원형덕트경 34를 감당하는 단변 35cm로 하는 장변은 35cm인 38.3 칸 밖에 없어서 그대로 구하는 것으로 판단할 수 있지만

이는 긴변과 짧은 변에 해당하는 원형덕트경 환산표이므로

한변이(높이) 350mm 이 되는 사각 덕트를 구해야 합니다.

따라서, 환산표에서 원형 덕트경 34cm에 해당하는 장변과 단변을 찾아 보면 단변을 한치수 낮추어 30cm을 했을 때 높이에 해당하는 원형덕트 경(34보다 큰 35.4 칸)의 장변은 35cm를 구할 수 있습니다.

결국 마지막 C-D구간은 장변 35cm를 높이로 하는 단변을 구하게 되었습니다.

그래서 장변 35cm가 높이(H) 이고 단변 30cm는 덕트의 폭(W)이 됩니다.

(환산표 참조)

여기서 답란을 작성 할 때는 오른쪽이 높이에 해당하는 위치이기 때문에 30×35로 답을 해야 합니다.

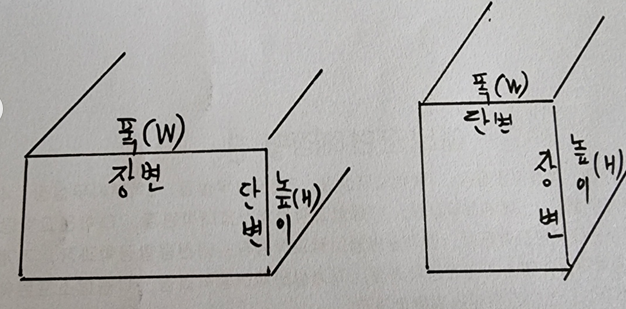
참고로 덕트는 긴변이 장변 짧은 변이 단변입니다.

그리고 수평 도면상의 덕트크기가 폭(W)이 되고 수직상의 길이가 높이(H)가 됩니다.

일반적으로 각형 덕트는 장변과 단변에서 많은 덕트들은 장변이 폭(W)이고 단변이 높이(H)이지만 이 문제의 C-D구간은 폭이 단변이 되는 덕트가 되며 답란에는 높이를 일정하게 답해야 하므로 단순히 장변과 단변을 답하는 것이 아닌 폭과 높이로 답을 해야 합니다.

    (그림 참조)

401페이지 15번

분기부와 굴곡부의 국부저항은 계산법이 다릅니다. 

상기 문제처럼 굴곡부는 굴곡부 덕트경의 몇 배수에 해당하는 상당길이로 계산하는 법이 있기 때문에 해당문제처럼 조건이 주어지면 굴곡부 만 계산하게 됩니다.

하지만 분기부에서도 국부손실이 발생하는데 다른 계산법을 주면 복잡해 질 수 있어서 분기부도 굴곡부에 해당된다라는 조건을 주게 되는데 이때는 분기부를 굴곡부처럼 해석하여 포함하여 계산해야 합니다.

따라서 수험자 입장에서는 헷갈리는 부분입니다.

또한 국부저항에서 해당구간의 풍속과 국부저항계수를 곱하여 손실을 구하는 경우가 있는데 이때는 분기부나 굴곡부 모두 이 공식을 이용합니다, 다만 국부저항계수는 다릅니다.

그래서 국부저항계수를 이용할 때 분기부와 굴곡부 조건이 없으면 모두 적용하고 분기부의 저항계수는 이라고 명시하면 분기부만 적용하여 문제를 풀게 됩니다.

덕트부 분기나 굴곡부에서는 일반화된 하나의 공통된 공식이 적용되는 것이 아니다 보니 수험생들이 문제를 해석하는데 어려워 하고 있습니다.

예제문제를 많이 풀어보시기 바랍니다.